how to find slope with two sets of coordinates
Finding the Slope of a Line
Encyclopaedism Objective(s)
· Bump the slope of a line from a graph.
· Find the slope of a line given ii points.
· Find the slope of the lines x = a and y = b.
Founding
The idea of pitch is something you happen often in everyday life. Flirt with wheeling a cart down a ramp or climbing a set of stairs. Both the ramp and the stairs have a gradient. You can discover the pitch, or precipitousness, of the incline and stairs past considering level and steep movement on them. In conversation, you use run-in similar "gradual" or "steep" to describe slope. Along a gradual slope, most of the motion is flat. Along a steep pitch, the upright movement is greater.
The mathematical definition of slope is very look-alike to our unremarkable one. In math, slope is put-upon to describe the steepness and direction of lines. By just looking at the graph of a line of merchandise, you can learn or s things about its slope, especially proportionate to other lines graphed on the same organise shave. Consider the graphs of the three lines shown below:
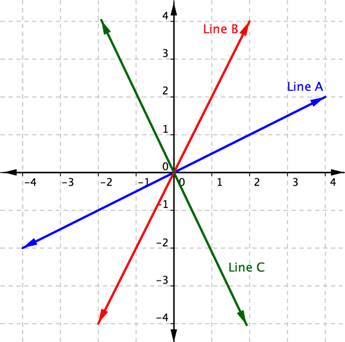
Foremost, let's look at lines A and B. If you imagined these lines to embody hills, you would say that line B is steeper than demarcation A. Personal line of credit B has a greater slope than line A.
Next, notice that lines A and B slant up every bit you go up from left to right. We say these ii lines have a affirmatory slope. Line of reasoning C slants down from left to right. Line C has a Gram-negative slope. Victimization ii of the points on the origin, you can find the slope of the origin by determination the rise and the play. The vertical change between deuce points is known as the salary increase, and the horizontal exchange is called the run. The slope equals the rise sectioned by the run: ![]() .
.
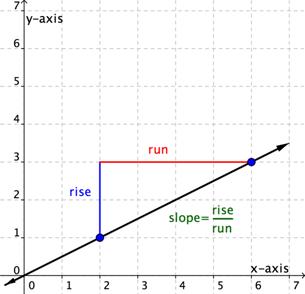
Determination the Slope of a Line from a Graph
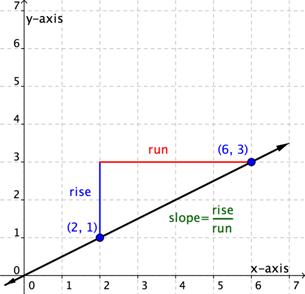
You can determine the slope of a line from its graph by look the rise and prevail. Same characteristic of a parentage is that its slope is constant all the way along IT. Then, you can prefer any 2 points on the graph of the line to figure out the slope. Army of the Righteou's view an example.
| Example | ||
| Trouble | Use the graph to rule the gradient of the line. | |
| rise = 2 | Start from a point on the line, such equally (2, 1) and move vertically until in line with another point on the line, so much equally (6, 3). The prove is 2 units. Information technology is positive American Samoa you moved up. | |
| run = 4 | Next, move horizontally to the point (6, 3). Numerate the routine of units. The run is 4 units. Information technology is positive A you moved to the right. | |
| Slope = | Gradient = | |
| Answer | The side is | |
This line will undergo a slope of ![]() none matter which two points you plectron connected the line. Try mensuration the slope from the origin, (0, 0), pertinent (6, 3). You will find that the rise = 3 and the run = 6. The slope is
none matter which two points you plectron connected the line. Try mensuration the slope from the origin, (0, 0), pertinent (6, 3). You will find that the rise = 3 and the run = 6. The slope is ![]() . It is the same!
. It is the same!
Let's wait at another example.
| Example | ||||
| Problem | Use the graph to find the slope of the two lines. | |||
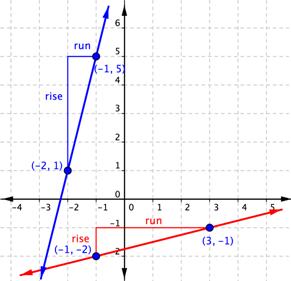
| Notice that both of these lines wealthy person positive slopes, sol you expect your answers to be empiricist philosophy. | ||||
| rise = 4 | Gloomy line Beginning with the blue transmission line, going from guide (-2, 1) to point (-1, 5). This descent has a rise of 4 units finished, so IT is positive. | |||
| running play = 1 | Outpouring is 1 unit to the moral, so it is positive. | |||
| Incline = | Substitute the values for the rear and run in the recipe Side = | |||
| rise = 1 | Red pedigree The red line, going from point (-1, -2) to point (3, -1) has a rise of 1 unit of measurement. | |||
| run = 4 | The red line has a run of 4 units. | |||
| Slope = | Substitute the values for the rise and run into the rul Slope = | |||
| Answer | The side of the blue line is 4 and the slope of the bloody job is | |||
When you look at the two lines, you can see that the blue short letter is steeper than the red line. It makes horse sense the prize of the gradient of the blue line, 4, is greater than the respect of the slope of the red line, ![]() . The greater the slope, the steeper the line.
. The greater the slope, the steeper the line.
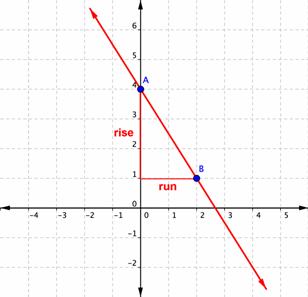
The next illustration shows a line with a Gram-negative slope.
| Example | ||
| Problem | Find the slope of the line graphed below. | |
| rise = − 3 | Start at Point A, (0, 4) and rise − 3. This agency moving 3 units in a disconfirming direction. | |
| endure = 2 | From there, run 2 units in a positive direction to Point B (2, 1). | |
| Slope = | Gradient = | |
| Answer | The slope of the line is | |
Direction is important when it comes to determining slope. It's important to pay attention to whether you are moving heavenward, down, leftmost, or conservative; that is, if you are moving in a positive or negative direction. If you go up to get to your endorsement sharpen, the rise is positive. If you go down to get to your second point, the rise is unfavorable. If you go precise to get to your second point, the run is positive. If you fling left to get to your intermediate point, the run is negative. In the model preceding, you could hold found the pitch by starting at point B, running − 2, and then rising +3 to arrive at point A. The result is still a incline of ![]() .
.
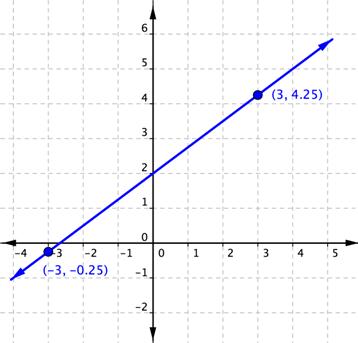
| Advanced Deterrent example | ||
| Trouble | Find the slope of the line of credit graphed to a lower place. | |
| rise = 4.5 | Embark on at (-3, -0.25) and acclivity 4.5 . This means moving 4.5 units in a positive focal point. | |
| run = 6 | From there, operate 6 units in a positive commission to (3, 4.25). | |
| | | |
| Answer | The slope of the line is 0.75. | |
Looking at Equations
The slope of a line hindquarters sometimes be quickly determined from its equation. Let's consider the line whose equation is y = 5x. You can create a table of values to find oneself 3 points along the dividing line.
Plotting these points, create the graph of the line and determine the pitch.
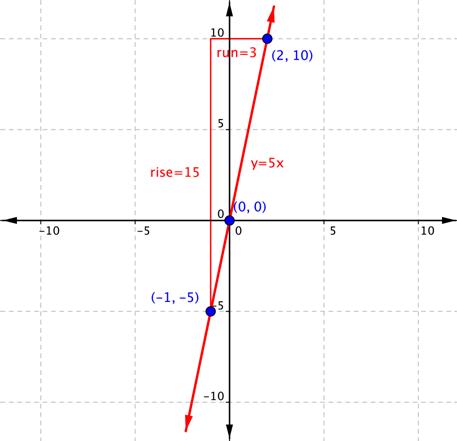
American Samoa you move from the point (-1, -5) to the point (2, 10), the line has a rise of 15 and a tend of 3, so the slope of the air is ![]() . Notice that the number 5 also appears in the equality: y = 5x.
. Notice that the number 5 also appears in the equality: y = 5x.
Whenever the equality of a line of reasoning is codified in the spring y = mx + b, it is called the slope-intercept form of the equation. The m is the slope of the line. And b is the b in the point that is the y-stop (0, b).
For example, for the par y = 3x – 7, the slope is 3, and the y-intercept is (0, −7).
What if the equation is written as 2y = 5x + 1? Then you essential rewrite the equation in the form y = Mx + b. Solve for y.
2y = 5x + 1
y = ![]() divide both sides of the equation by 2.
divide both sides of the equation by 2.
The gradient is ![]() , and the y-intercept is (0,
, and the y-intercept is (0, ![]() ).
).
What is the slope of the line whose equation is y = −2x + 7?
A) 7
B) 2
C) −2
D) ![]()
Display/Hide Answer
A) 7
Incorrect. The slope for a line written in y = mx + b is given by the coefficient of x. The right-minded solution is −2.
B) 2
Inaccurate. The slope for a line written in y = mx + b is given by the coefficient of x. The coefficient is −2. The correct solution is −2.
C) −2
Correct. The slope for a line written in y = mx + b is given away the coefficient of x. For this line the coefficient, or m, the slope, is −2.
D) ![]()
Incorrect. The gradient for a melody written in y = mx + b is given past the coefficient of x. The coefficient is −2. The correct answer is −2.
Finding the Pitch of a Line Relinquished Two Points
You've seen that you can find the slope of a line on a graph by measure the get up and the run. You can likewise find the slope of a straight demarcation without its graph if you know the coordinates of whatever deuce points thereon describe. Every point has a set of coordinates: an x-value and a y-measure, codified Eastern Samoa an ordered duo (x, y). The x value tells you where a point is horizontally. The y economic value tells you where the point is vertically.
Consider two points on a line—Point 1 and Point 2. Pointedness 1 has coordinates (x 1, y 1) and Stop 2 has coordinates (x 2, y 2).
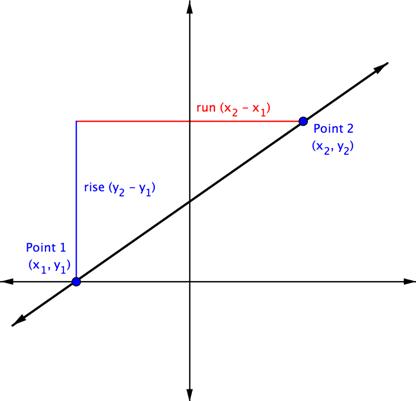
The rise is the orthostatic distance 'tween the deuce points, which is the dispute between their y-coordinates. That makes the emanation y 2 − y 1. The run between these two points is the difference in the x-coordinates, or x 2 − x 1.
So, ![]() operating theatre
operating theatre ![]()
In the example below, you'll see that the line has two points each indicated American Samoa an ordered pair. The point (0, 2) is indicated as Point 1, and (−2, 6) as Charge 2. So you are going away to move from Point 1 to Point 2. A trilateral is drawn in to a higher place the descent to help illustrate the rise and run.
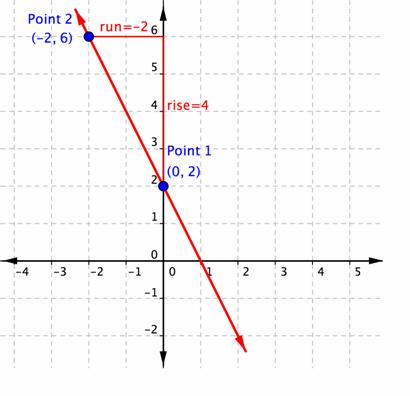
You posterior figure from the graph that the rise going from Point 1 to Point 2 is 4, because you are moving 4 units in a positive counsel (up). The consort is −2, because you are then moving in a negative direction (left) 2 units. Using the gradient formula, ![]() .
.
You do not need the graph to find the slope. You throne scarce use the coordinates, keeping careful give chase of which is Point 1 and which is Head 2. Let's organize the information about the two points:
| Epithet | Ordered Twain | Coordinates |
| Sharpen 1 | (0, 2) | x 1 = 0 y 1 = 2 |
| Compass point 2 | ( −2 , 6) | x 2 = -2 y 2 = 6 |
The slope, ![]() =
= ![]() . The slope of the line, m, is −2.
. The slope of the line, m, is −2.
Information technology doesn't matter which stop is designated as Point 1 and which is Maneuver 2. You could have called (−2, 6) Point 1, and (0, 2) Power point 2. In that case, putting the coordinates into the pitch normal produces the equation ![]() . Once more, the slope m = −2. That's the same side as before. The important thing is to be consistent when you subtract: you essential always subtract in the same order y 2 − y 1 and x 2 − x 1.
. Once more, the slope m = −2. That's the same side as before. The important thing is to be consistent when you subtract: you essential always subtract in the same order y 2 − y 1 and x 2 − x 1.
| Example | ||
| Problem | What is the slope of the line that contains the points (5, 5) and (4, 2)? | |
| x 1 = 4 y 1 = 2 | (4, 2) = Point 1, (x 1, y 1) | |
| x 2 = 5 y 2 = 5 | (5, 5) = Point 2, (x 2, y 2) | |
| m = 3 | Substitute the values into the side formula and simplify. | |
| Answer | The slope is 3. | |
The example below shows the solution when you reversal the order of the points, calling (5, 5) Point 1 and (4, 2) Point 2.
| Case | ||
| Problem | What is the gradient of the line of reasoning that contains the points (5, 5) and (4, 2)? | |
| x 1 = 5 y 1 = 5 | (5, 5) = Point 1, (x 1, y 1) | |
| x 2 = 4 y 2 = 2 | (4, 2) = Breaker point 2, (x 2, y 2) | |
| m = 3 | Substitute the values into the slope rule and simplify. | |
| Resolution | The gradient is 3. | |
Placard that regardless of which ordered twin is named Point 1 and which is named Full point 2, the slope is still 3.
| Advanced Representative | ||
| Problem | What is the slope of the line that contains the points (3,-6.25) and (-1,8.5)? | |
| | (3,-6.25) = Point 1, | |
| | (-1,8.5) = Point 2, | |
| | Substitute the values into the slope formula and simplify. | |
| Answer | The slope is -3.6875. | |
What is the gradient of a line that includes the points (−5, 1) and (−2, 3)
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Show/Hide Answer
A) ![]()
Correct. ![]()
B) ![]()
Erroneous. The denominator is −2 − (−5), not −2 − 5. The correct solvent is ![]() .
.
C) ![]()
Incorrect. Put the coordinates into the slope expression consistently: ![]() . The word-perfect answer is
. The word-perfect answer is ![]() .
.
D) ![]()
Incorrect. You have interchanged the rise and the run. The correct answer is ![]() .
.
Advanced Question
What is the slope of a line that includes the points ![]() and
and ![]() ?
?
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Show/Enshroud Answer
A) ![]()
Incorrect. It looks like you inverted the rise and the hunt. Use the formula ![]() to find the gradient. The precise answer is
to find the gradient. The precise answer is ![]() .
.
B) ![]()
Incorrect. Information technology looks the like you subtracted either the y or x coordinates in the wrong order. Make a point you deduct ![]() , then
, then ![]() , and and then calculate the pitch. The correct answer is
, and and then calculate the pitch. The correct answer is ![]() .
.
C) ![]()
Incorrect. It looks like you subtracted either the y operating room x coordinates in the wrong plac. Make a point you take off ![]() , then
, then ![]() , and then calculate the gradient. The correct answer is
, and then calculate the gradient. The correct answer is ![]() .
.
D) ![]()
Correct. Using the formula for slope, ![]() , you found that
, you found that  .
.
Finding the Slopes of Horizontal and Vertical Lines
So far you've considered lines that lean "uphill" surgery "downhill." Their slopes may constitute unconscionable or gradatory, but they are always positive or negative numbers. Just there are two new kinds of lines, horizontal and vertical. What is the slope of a flat line Oregon level ground? Of a wall or a vertical line?
Let's consider a level line on a graph. No matter which two points you choose on the line, they will forever cause the same y-ordinate. The equation for this line is y = 3. The par can also embody written equally y = (0)x + 3.

Victimisation the form y = 0x + 3, you can see that the slope is 0. You can also use the slope formula with two points on this naiant channel to calculate the slope of this horizontal communication channel. Using (−3, 3) American Samoa Point 1 and (2, 3) as Point 2, you get:
![]()
![]()
The slope of this horizontal seam is 0.
Let's consider some horizontal line. Irrespective which two points you choose on the line, they leave always have the one y-coordinate. So, when you apply the slope chemical formula, the numerator will always be 0. Zero divided by any not-zilch come is 0, so the slope of any flat line is e'er 0.
The equating for the horizontal line y = 3 is apprisal you that no matter which two points you choose on this assembly line, the y-coordinate will always be 3.
How about vertical lines? In their case, no matter which two points you select, they wish e'er have the indistinguishable x-coordinate. The equation for this line is x = 2.
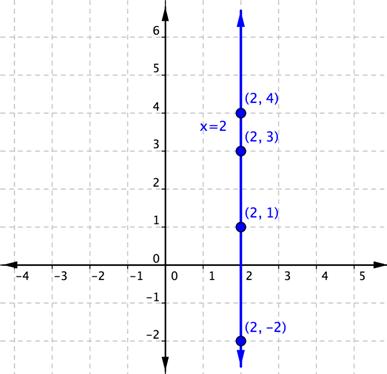
There is atomic number 102 way that this equation can be put in the slope-point frame, as the coefficient of y is 0 (x = 0y + 2).
Indeed, what happens when you usage the gradient rule with two points on this vertical trace to calculate the incline? Using (2, 1) as Point in time 1 and (2, 3) as Point 2, you amaze:
![]()
![]()
Just division by zero point has zero meaning for the set of real numbers. Because of this fact, it is aforesaid that the incline of this vertical line of merchandise is undefined. This is true for each vertical lines— they all have a slope that is undefined.
| Case | ||
| Problem | What is the slope of the line that contains the points (3, 2) and ( − 8, 2)? | |
| | (3, 2) = Point 1, | |
| | ( − 8, 2) = Point 2, | |
| m = 0 | Replacement the values into the slope formula and simplify. | |
| Answer | The slope is 0, so the line is horizontal. | |
Advanced Question
Which of the following points will lie on the line created by the points ![]() and
and ![]() ?
?
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Evince/Hide Response
A) ![]()
Incorrect. Poster that both points on the line have the comparable x-co-ordinate but polar y-coordinates. That makes it a vertical line, so whatever other points on the origin will make an x-coordinate of -3.75. The correct reply is ![]() .
.
B) ![]()
Make up. The points ![]() and
and ![]() form a vertical telephone circuit, and so any other point on that line will have to have an x-coordinate of -3.75.
form a vertical telephone circuit, and so any other point on that line will have to have an x-coordinate of -3.75.
C) ![]()
Incorrect. Try drawing a spry sketch of the points ![]() and
and ![]() . They form a vertical tune, so any other points on the line bequeath experience an x-align of -3.75. The correct respond is
. They form a vertical tune, so any other points on the line bequeath experience an x-align of -3.75. The correct respond is ![]() .
.
D) ![]()
Incorrect. Notice that both points along the line of descent have the same x-align but different y-coordinates. That makes it a vertical line, so any other points along the descent will have an x-coordinate of -3.75. The counterbalance answer is ![]() .
.
Compendious
Slope describes the steepness of a line. The slope of any line remains constant along the line. The slope can also tell you information about the direction of the line on the coordinate planing machine. Slope can personify calculated either past looking for at the chart of a rail line or by using the coordinates of whatever two points on a line. There are two common formulas for slope: Slope = ![]() and
and ![]() where m = slope and
where m = slope and ![]() and
and ![]() are two points on the air.
are two points on the air.
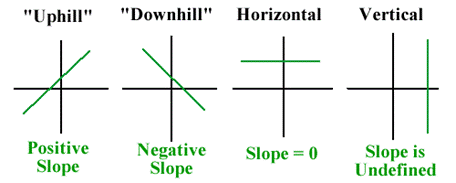
The images below summarize the slopes of different types of lines.
how to find slope with two sets of coordinates
Source: https://www.montereyinstitute.org/courses/DevelopmentalMath/COURSE_TEXT2_RESOURCE/U13_L2_T1_text_final.html
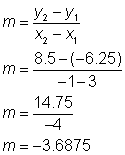
Posting Komentar untuk "how to find slope with two sets of coordinates"